Yttrium Insights Part 1: Traversing a Math System

Yttrium models basically are arbitrary bipartite directed graphs with ports on one and signals (and buses) on the other side. Signals connect ports with each other in any way, including loops and cycles.

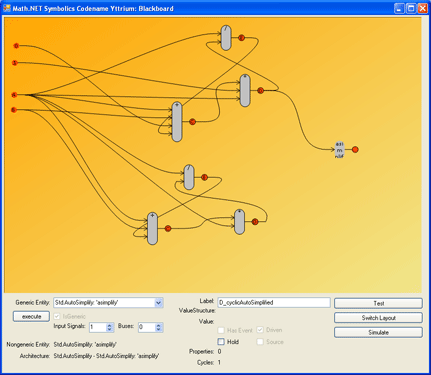
The screenshot above shows two cyclic models with three ports each (divide, add, multiply - click on the image to zoom in), where signal E depends on (A,D), signal D depends on (A,C) and signal C depends on (A,B,E), closing the cycle. The lower model is a simplified version of the upper: two pointless operations (adding constant 0 and multiply by a constant 1) are removed. This was automatically generated by the attached "asimplify" port in the upper model (it generated the lower D as a simplified version of the upper D). Although this sounds simple, it's quite a complex operation. For this and nearly all other operations on a model one needs a proper way to traverse the model. This could be programmed manually for every operation as the signals know their source port (but not their target ports) and the ports know both input and output signals, but that's hardly an option as programming it should be "simple".

Traversing Graphs

Often, traversing is implemented with the iterator pattern. Iterators are perfectly supported by the .NET framework and C# 2.0 (Enumerator classes and interfaces, foreach, yield). However, there are multiple ways to walk through a tree (classical: in-order, pre-order and post-order), and even more to walk though cyclic graphs. Some algorithms just need to iterate though all signals in arbitrary order, others need spanning trees or even all possible (non-cyclic) paths to a given signal or port. Some algorithms want to stop following the current path on some special conditions. In short, there are quite a few ways to iterate a system. To keep it customizable and extensible we move the actual iterator logic to separate classes in terms of the strategy pattern. You may implement your own strategies, but I already implement five strategies:

• All Signals (every signal only once)
• All Ports
• Spanning Tree
• All Paths (from any node to the given root node)
• All (completely controllable by the visitor, see below)

Do Something While Traversing

Of course it's only interesting to traverse a graph if you can actually do something with the elements. Because our graph is not homogeneous, the we can't just "yield" any items found. Instead, the strategies take along visitors who visit any elements the strategy passes. This is the classical visitor pattern. Again there are several predefined visitors available:

• SignalActionVisitor (does something with every signal)
• PortActionVisitor
• SignalConditionalActionVisitor
• PortConditionalActionVisitor
• CollectVisitor (collects any Signals/Buses/Ports visited)
• ConditionalCollectVisitor
• SignalPathCollectVisitor (collects any paths to a signal as a list of signal-lists)
• PortPathCollectVisitor<
• ExistsSignalVisitor (to check whether a signal matches a predicate)
• ExistsPortVisitor
• TrueForAllSignalsVisitor (to check whether all signals match a predicate)
• TrueForAllPortsVisitor

Manipulation System

In a computer algebra system you may want to substitute some elements, simplify or derive algebraic systems, apply trigonometric conversions and so on. In all this cases you need to manipulate the system, or more exactly build a new signal tree without touching the existing tree but reusing as much as possible. For example, if you substitute a signal only one of the root operands depend on, you don't want to clone the other operands, only the depending one. Most of the complexity of this process is common to all operations, e.g. the handling of cycles and cyclic dependencies.

The Manipulator class provides a solution based on the traversing system introduced above. It introduces a new kind of second order visitors, IManipulationVisitor. You may implement your own manipulation visitors, but often it's easier to provide transformations in terms of the theorems subsystem. transformation theorems (ITransformationTheorem) are executed using the TransformationManipulatorVisitor (implements IManipulationVisitor) and the Manipulator class.

The standard package provides three transformation theorem types at the moment:

• AutoSimplify (automatic simplification)
• Derive (algebraic derivation)
• TrigonometricSubstitute (e.g. transform csc(x) to 1/sin(x))