What's New in Math.NET Numerics 2.6
Math.NET Numerics v2.6, released in July 2013, is focused on filling some gaps around the very basic numerical problems of fitting a curve to data and finding solutions of nonlinear equations. As usual you'll find a full listing of all changes in the release notes. However, I'd like to take the chance to highlight some important changes, show some code samples and explain the reasoning behind the changes.
A lot of high quality code contributions made this release possible. Just like last release, I've tried to attribute them directly in the release notes. Thanks again!
Please let me know if these "What's New" articles are useful in this format and whether I should continue to put the together for future releases. See also what's new in the previous version 2.5.
Linear Curve Fitting
Fitting a linear-parametric curve to a set of samples such that the squared errors are minimal has always been possible with the linear algebra toolkit, but it was somewhat complicated to do and required understanding of the algorithm. See Linear Regression with Math.NET Numerics for an introduction and some examples.
Note: if you need to have the curve go exactly through all your data points, use our Interpolation routines instead.
We now finally provide a shortcut with a few common functions to fit to data, but also a method to fit a linear combination of arbitrary functions. For fitting a simple line it uses an efficient direct algorithm:
1: 2: 3: 4: 5: 6: 7: 8: |
|
Otherwise it usually applies an ordinary least squares regression to find the best parameters using a thin QR decomposition (leveraging a native provider like Intel MKL if enabled). This also works with arbitrary functions, like sine and cosine:
1: 2: 3: 4: |
|
The intention is to add more special cases for common curves like the logistic function in the future. Like the line they may have more appropriate direct implementations. For now there is one other special case, for fitting to a polynomial. It returns the best parameters, in ascending order (coefficient for power k has index k) compatible to the Evaluate.Polynomial routine:
1: 2: 3: |
|
In practice your x values are not always just real numbers. Maybe you need multi-dimensional fitting where the x values are actually arrays, or even full data structures. For such cases we provide a version that is generic in x and where you can provide a list of functions that accept such x directly without the need to convert to an intermediate double vector first:
1: 2: 3: |
|
Often after evaluating the best fitting linear parameters you'd actually want to evaluate the function with those parameters. For this scenario we provide a shortcut as well: For each of these methods there is also a version with a "Func" suffix ("F" in F#) which, instead of the parameters, returns the composed function:
1: 2: 3: 4: 5: |
|
Root Finding
We now provide basic root finding algorithms. A root of a function x -> f(x) is a solution of the equation f(x)=0. Root-finding algorithms can thus help finding numerical real solutions of arbitrary equations, provided f is reasonably well-behaved and we already have an idea about an interval [a,b] where we expect a root. As usual, there is a facade class FindRoots for simple scenarios:
The routines usually expect a lower and upper boundary as parameters, and then optionally the accuracy we try to achieve and the maximum number of iterations.
1: 2: 3: 4: 5: 6: |
|
A NonConvergenceException is thrown if no root can be found by the algorithm.
In practice you'd often want to use a specific well-known algorithm. You'll find them in the RootFinding namespace. Each of these algorithm provides a FindRoot method with similar arguments as those above. However, the algorithms may sometimes fail to find a root or the function may not actually have a root within the provided interval. Failing to find a root is thus not exactly exceptional. That's why the algorithms also provide an exception-free TryFindRoot code path with the common Try-pattern as in TryParse.
Bisection
A simple and robust yet rather slow algorithm, implemented in the Bisection class.
Example: Find the real roots of the cubic polynomial 2x^3 + 4x^2 - 50x + 6:
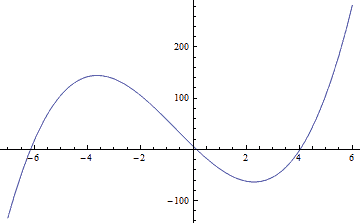
1: 2: 3: 4: 5: 6: |
|
Note that the F# function returns a float option. Instead of throwing an exception it will simply return None if it fails.
Brent's Method
We use Brent's method as default algorithm, implemented in the Brent class. Brent's method is faster than bisection, but falls back to something close to bisection if the faster approaches (essentially the secant method and inverse quadratic interpolation) fails and is therefore almost as reliable.
The same example as above, but using Brent's method:
1: 2: 3: 4: 5: 6: |
|
Note that there are better algorithms for finding all roots of a polynomial. We plan to add specific polynomial root finding algorithms later on.
Newton-Raphson
The Newton-Raphson method leverages the function's first derivative to converge much faster, but can also fail completely. The pure Newton-Raphson algorithm is implemented in the NewtonRaphson class. However, we also provide a modified algorithm that tries to recover (instead of just failing) when overshooting, converging too slowly or even when loosing bracketing in the presence of a pole. This modified algorithms is available in the RobustNewtonRaphson class.
Example: Assume we want to find solutions of x+1/(x-2) == -2, hence x -> f(x) = 1/(x-2)+x+2 with a pole at x==2:
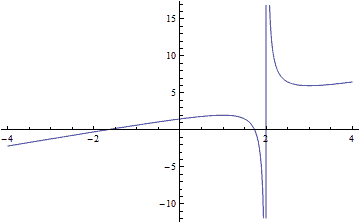
1: 2: 3: 4: 5: 6: 7: 8: 9: |
|
Broyden's Method
The quasi-newton method by Broyden, implemented in the Broyden class, may help you to find roots in multi-dimensional problems.
Linear Algebra
As usual there have been quite a few improvements around linear algebra, see the release notes for the complete list. If you've enabled our Intel MKL native linear algebra provider, then eigenvalue decompositions should be much faster now. Matrices now also support the new F# 3.1 array slicing syntax.
Note that we're phasing out the MathNet.Numerics.IO library and namespace and plan to drop it entirely in v3. We've already replaced it with two new separate NuGet packages and obsoleted all members of the old library. The new approach with separate libraries makes it possible to introduce specific dependencies e.g. to read and write Excel files, without forcing these dependencies on all of Math.NET Numerics. We recommend to switch over to the new packages as soon as possible.
Statistics
We've had a Pearson correlation coefficient routine for a while, but no Covariance routine. In addition to a new Spearman ranked correlation routine, this release finally also adds sample and population Covariance functions for arrays and IEnumerables.
1:
|
|
module List
from Microsoft.FSharp.Collections
--------------------
type List<'T> =
| ( [] )
| ( :: ) of Head: 'T * Tail: 'T list
interface IEnumerable
interface IEnumerable<'T>
member GetSlice : startIndex:int option * endIndex:int option -> 'T list
member Head : 'T
member IsEmpty : bool
member Item : index:int -> 'T with get
member Length : int
member Tail : 'T list
static member Cons : head:'T * tail:'T list -> 'T list
static member Empty : 'T list
Full name: Microsoft.FSharp.Collections.List<_>
Full name: Microsoft.FSharp.Collections.List.map
val double : value:'T -> double (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.ExtraTopLevelOperators.double
--------------------
type double = System.Double
Full name: Microsoft.FSharp.Core.double